Triângulo Retângulo: Decifrando a Hipotenusa, os Catetos e o Teorema de Pitágoras -

O Protagonista da Geometria: O Triângulo Retângulo

No vasto universo da geometria, poucas figuras são tão icônicas e úteis quanto o triângulo retângulo. Mas o que o torna tão especial? A resposta está em um de seus ângulos: ele possui um ângulo interno de exatamente 90°, conhecido como “ângulo reto”. É essa característica que define seu nome e abre as portas para uma das relações matemáticas mais famosas do mundo.

Qualquer triângulo que possui um canto perfeitamente “quadrado”, como o canto de um livro ou de uma sala, é um triângulo retângulo. Seus lados recebem nomes especiais que são fundamentais para entendê-lo.

Conhecendo os Lados: Hipotenusa e Catetos

Os três lados de um triângulo retângulo não são iguais em status. Eles são classificados com base em sua posição em relação ao ângulo reto de 90°.

Catetos: São os dois lados que formam o ângulo reto. Pense neles como os dois “braços” que se encontram para criar o canto de 90°. Em qualquer triângulo retângulo, sempre haverá dois catetos.
Hipotenusa: É o lado oposto ao ângulo reto. Uma dica fácil para identificá-la é que a hipotenusa é sempre o maior lado do triângulo retângulo. Ela “fecha” o triângulo, conectando as pontas dos dois catetos.

Identificar corretamente quem é quem é o primeiro passo para dominar os cálculos envolvendo essa figura geométrica.

A Relação Mágica: O Teorema de Pitágoras

Os antigos gregos, em especial o matemático Pitágoras, descobriram uma relação incrível e imutável entre os lados de qualquer triângulo retângulo. Essa relação ficou conhecida como o Teorema de Pitágoras.

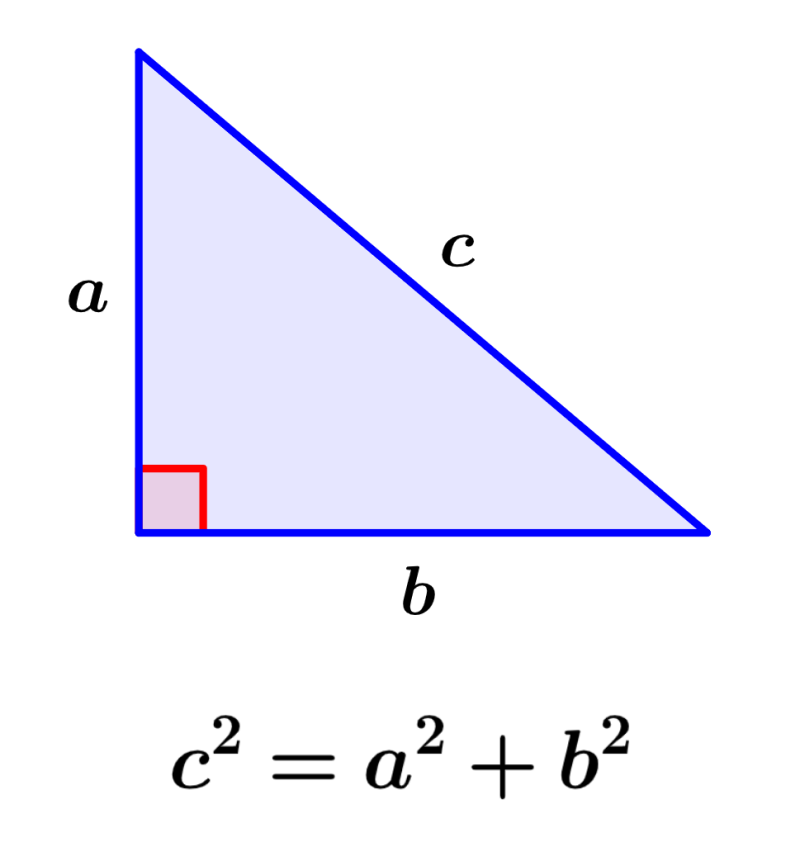
O teorema afirma que: “O quadrado da medida da hipotenusa é igual à soma dos quadrados das medidas dos catetos.”

Essa regra é a chave para encontrar a medida de um lado desconhecido quando conhecemos os outros dois. A fórmula é a seguinte:

Onde:

a é a hipotenusa
b e c são os catetos

Exemplo Prático:

Imagine um triângulo retângulo onde os catetos medem 3 cm e 4 cm. Qual o tamanho da hipotenusa?

Identifique os dados: cateto (b) = 3, cateto (c) = 4, hipotenusa (a) = ?
Aplique a fórmula: $a^{2} = b^{2} + c^{2}$
Substitua os valores: $a^{2} = 3^{2} + 4^{2}$
Calcule os quadrados: $a^{2} = 9 + 16$
Some os resultados: $a^{2} = 25$
Encontre a raiz quadrada: $a = s q r t 25$
Resultado: $a = 5$ cm

Portanto, a hipotenusa mede 5 cm. Essa mesma lógica pode ser usada para encontrar o valor de um cateto se a hipotenusa for conhecida.

Videoaula para Aprofundar

Para ver esses conceitos em ação com uma explicação detalhada, assista a esta excelente videoaula sobre o Teorema de Pitágoras:

Conclusão

O triângulo retângulo, com seus catetos e hipotenusa, é uma peça fundamental não apenas na matemática escolar, mas em diversas aplicações práticas, como na engenharia, arquitetura, design e até mesmo na navegação por GPS. Entender o Teorema de Pitágoras não é apenas decorar uma fórmula, mas sim compreender uma das lógicas mais elegantes e poderosas da geometria.